Esta es la Segunda Unidad de Física, los temas se describen a continuación:
LEYES DE NEWTON.
| Primera ley o ley de inercía | Todo cuerpo permanece en su estado de reposo o de movimiento rectilíneo uniforme a menos que otros cuerpos actúen sobre él. |
| Segunda ley o Principio Fundamental de la Dinámica | La fuerza que actua sobre un cuerpo es directamente proporcional a su aceleración. |
| Tercera ley o Principio de acción-reacción | Cuando un cuerpo ejerce una fuerza sobre otro, éste ejerce sobre el primero una fuerza igual y de sentido opuesto. |

La primera ley de Newton, conocida también como Ley de inercía, nos dice que si sobre un cuerpo no actua ningún otro, este permanecerá indefinidamente moviéndose en línea recta con velocidad constante (incluido el estado de reposo, que equivale a velocidad cero).
Como sabemos, el movimiento es relativo, es decir, depende de cual sea el observador que describa el movimiento. Así, para un pasajero de un tren, el interventor viene caminando lentamente por el pasillo del tren, mientras que para alguien que ve pasar el tren desde el andén de una estación, el interventor se está moviendo a una gran velocidad. Se necesita, por tanto, un sistema de referencia al cual referir el movimiento. La primera ley de Newton sirve para definir un tipo especial de sistemas de referencia conocidos como Sistemas de referencia inerciales, que son aquellos sistemas de referencia desde los que se observa que un cuerpo sobre el que no actúa ninguna fuerza neta se mueve con velocidad constante.
En realidad, es imposible encontrar un sistema de referencia inercial, puesto que siempre hay algún tipo de fuerzas actuando sobre los cuerpos, pero siempre es posible encontrar un sistema de referencia en el que el problema que estemos estudiando se pueda tratar como si estuviésemos en un sistema inercial. En muchos casos, suponer a un observador fijo en la Tierra es una buena aproximación de sistema inercial.
La Primera ley de Newton nos dice que para que un cuerpo altere su movimiento es necesario que exista algo que provoque dicho cambio. Ese algo es lo que conocemos como fuerzas. Estas son el resultado de la acción de unos cuerpos sobre otros.
La Segunda ley de Newton se encarga de cuantificar el concepto de fuerza. Nos dice que la fuerza neta aplicada sobre un cuerpo es proporcional a la aceleración que adquiere dicho cuerpo. La constante de proporcionalidad es la masa del cuerpo, de manera que podemos expresar la relación de la siguiente manera:
Para ello primero vamos a definir una magnitud física nueva. Esta magnitud física es la cantidad de movimiento que se representa por la letra p y que se define como el producto de la masa de un cuerpo por su velocidad, es decir:
La Fuerza que actua sobre un cuerpo es igual a la variación temporal de la cantidad de movimiento de dicho cuerpo, es decir,
Tal como comentamos en al principio de la Segunda ley de Newton las fuerzas son el resultado de la acción de unos cuerpos sobre otros.
La tercera ley, también conocida como Principio de acción y reacción nos dice que si un cuerpo A ejerce una acción sobre otro cuerpo B, éste realiza sobre A otra acción igual y de sentido contrario.
Esto es algo que podemos comprobar a diario en numerosas ocasiones. Por ejemplo, cuando queremos dar un salto hacia arriba, empujamos el suelo para impulsarnos. La reacción del suelo es la que nos hace saltar hacia arriba.
Cuando estamos en una piscina y empujamos a alguien, nosotros tambien nos movemos en sentido contrario. Esto se debe a la reacción que la otra persona hace sobre nosotros, aunque no haga el intento de empujarnos a nosotros.
Hay que destacar que, aunque los pares de acción y reacción tenga el mismo valor y sentidos contrarios, no se anulan entre si, puesto que actuan sobre cuerpos distintos.
En realidad, es imposible encontrar un sistema de referencia inercial, puesto que siempre hay algún tipo de fuerzas actuando sobre los cuerpos, pero siempre es posible encontrar un sistema de referencia en el que el problema que estemos estudiando se pueda tratar como si estuviésemos en un sistema inercial. En muchos casos, suponer a un observador fijo en la Tierra es una buena aproximación de sistema inercial.
La Primera ley de Newton nos dice que para que un cuerpo altere su movimiento es necesario que exista algo que provoque dicho cambio. Ese algo es lo que conocemos como fuerzas. Estas son el resultado de la acción de unos cuerpos sobre otros.
La Segunda ley de Newton se encarga de cuantificar el concepto de fuerza. Nos dice que la fuerza neta aplicada sobre un cuerpo es proporcional a la aceleración que adquiere dicho cuerpo. La constante de proporcionalidad es la masa del cuerpo, de manera que podemos expresar la relación de la siguiente manera:
F = m a
Tanto la fuerza como la aceleración son magnitudes vectoriales, es decir, tienen, además de un valor, una dirección y un sentido. De esta manera, la Segunda ley de Newton debe expresarse como:
F = m a
La unidad de fuerza en el Sistema Internacional es el Newton y se representa por N. Un Newton es la fuerza que hay que ejercer sobre un cuerpo de un kilogramo de masa para que adquiera una aceleración de 1 m/s2, o sea,
1 N = 1 Kg · 1 m/s2
La expresión de la Segunda ley de Newton que hemos dado es válida para cuerpos cuya masa sea constante. Si la masa varia, como por ejemplo un cohete que va quemando combustible, no es válida la relación F = m ·a. Vamos a generalizar la Segunda ley de Newton para que incluya el caso de sistemas en los que pueda variar la masa.Para ello primero vamos a definir una magnitud física nueva. Esta magnitud física es la cantidad de movimiento que se representa por la letra p y que se define como el producto de la masa de un cuerpo por su velocidad, es decir:
p = m · v
La cantidad de movimiento también se conoce como momento lineal. Es una magnitud vectorial y, en el Sistema Internacional se mide en Kg·m/s . En términos de esta nueva magnitud física, la Segunda ley de Newton se expresa de la siguiente manera:La Fuerza que actua sobre un cuerpo es igual a la variación temporal de la cantidad de movimiento de dicho cuerpo, es decir,
F = dp/dt
De esta forma incluimos también el caso de cuerpos cuya masa no sea constante. Para el caso de que la masa sea constante, recordando la definición de cantidad de movimiento y que como se deriva un producto tenemos:
F = d(m·v)/dt = m·dv/dt + dm/dt ·v
Como la masa es constante
dm/dt = 0
y recordando la definición de aceleración, nos queda
F = m a
tal y como habiamos visto anteriormente.
Otra consecuencia de expresar la Segunda ley de Newton usando la cantidad de movimiento es lo que se conoce como Principio de conservación de la cantidad de movimiento. Si la fuerza total que actua sobre un cuerpo es cero, la Segunda ley de Newton nos dice que:
0 = dp/dt
es decir, que la derivada de la cantidad de movimiento con respecto al tiempo es cero. Esto significa que la cantidad de movimiento debe ser constante en el tiempo (la derivada de una constante es cero). Esto es elPrincipio de conservación de la cantidad de movimiento: si la fuerza total que actua sobre un cuerpo es nula, la cantidad de movimiento del cuerpo permanece constante en el tiempo.Tal como comentamos en al principio de la Segunda ley de Newton las fuerzas son el resultado de la acción de unos cuerpos sobre otros.
La tercera ley, también conocida como Principio de acción y reacción nos dice que si un cuerpo A ejerce una acción sobre otro cuerpo B, éste realiza sobre A otra acción igual y de sentido contrario.
Esto es algo que podemos comprobar a diario en numerosas ocasiones. Por ejemplo, cuando queremos dar un salto hacia arriba, empujamos el suelo para impulsarnos. La reacción del suelo es la que nos hace saltar hacia arriba.
Cuando estamos en una piscina y empujamos a alguien, nosotros tambien nos movemos en sentido contrario. Esto se debe a la reacción que la otra persona hace sobre nosotros, aunque no haga el intento de empujarnos a nosotros.
Hay que destacar que, aunque los pares de acción y reacción tenga el mismo valor y sentidos contrarios, no se anulan entre si, puesto que actuan sobre cuerpos distintos.
Equilibrio traslacional
Seguramente estas familiarizado con la idea básica del concepto fuerza. De tu experiencia cotidiana sabes que aplicas una fuerza cuando jalas o empujas algún objeto. Cuando pateas un balón sabes que aplicas una fuerza. Tal vez creas que la fuerza se asocia con el movimiento, sin embargo, no siempre que se aplica una fuerza se produce movimiento. Si empujas una de las paredes de tu salón de clases verás que no se produce movimiento alguno a pesar del esfuerzo que haces.
Decimos que un objeto se encuentra en equilibrio si no esta acelerado. Por tanto el equilibrio considera dos situaciones: cuando el objeto esta reposo o bien cuando se mueve de una velocidad constante en una trayectoria rectilínea
Decimos que un objeto esta en equilibrio traslacional cuando se encuentra en reposo o bien se mueve en línea recta con velocidad constante.
Condiciones de equilibrio: Para que un cuerpo se encuentre en equilibrio, se requiere que la sumatoria de todas las fuerzas o torcas que actúan sobre él sea igual a cero. Se dice que todo cuerpo tiene dos tipos de equilibrio, el de traslación y el de rotación.
Traslación: Es aquel que surge en el momento en que todas las fuerzas que actúan sobre el cuerpo se nulifican, o sea, la sumatoria de las mismas sea igual a cero.
EFx = 0
EFy = 0
Rotación: Es aquel que surge en el momento en que todas las torcas que actúan sobre el cuerpo sean nulas, o sea, la sumatoria de las mismas sea igual a cero.
EMx= 0
EMy= 0
Aplicaciones: Se utiliza en todo tipo de instrumentos en los cuales se requiera aplicar una o varias fuerzas o torques para llevar a cabo el equilibrio de un cuerpo. Entre los instrumentos más comunes están la palanca,la balanza romana, la polea, el engrane, etc.

Problema del equilibrio traslacional
Una caja de 8 N está suspendida por un alambre de 2 m que forma un ángulo de 45° con la vertical. ¿Cuál es el valor de las fuerzas horizontal y en el alambre para que el cuerpo se mantenga estático?.
Primero se visualiza el problema de la siguiente manera: A continuación se elabora su diagrama de cuerpo libre.
A continuación se elabora su diagrama de cuerpo libre.
Ahora por medio de la descomposición de los vectores, calculamos la fuerza de cada uno de ellos.
F1x = - F1 cos 45°*
F1y = F1 sen 45°
F2x = F2 cos 0° = F2
F2y = F2sen0°=0
F3x = F3cos90°=0
F3y = - F3 sen 90° = - 8 N*
Porque los cuadrantes en los que se localizan son negativos.
Como únicamente conocemos los valores de F3, F2 y la sumatoria debe ser igual a cero en x e y, tenemos lo siguiente:
EFx=F1x+F2x+F3x=0
EFy=F1y+F2y+F3y=0
EFy=F1y+F2y+F3y=0
Por lo tanto tenemos lo siguiente:
EFx=-F1 cos 45+F2=0
F2=F1(0.7071)
EFy=-F1sen45-8N=0
8N=F1(0.7071)
F1=8N/0.7071=11.31 N
Para calcular F2, se sustituye F1 de la ecuación siguiente:
F2=F1(0.7071)
F2=11.31(0.7071)=8N
Equilibrio Rotacional
Es aquel equilibrio que ocurre cuando un cuerpo sufre un movimiento de rotacion o giro, al igual que el equilibrio traslacional debe tambien equilibrarse; surge en el momento en que todas las torcas que actúan sobre el cuerpo sean nulas, o sea, la sumatoria de las mismas sea igual a cero.
EMx= 0
EMy= 0
su fuerza se mide en torques o torcas es una magnitud (pseudo)vectorial, obtenida como producto vectorial del vector de posición del punto de aplicación de la fuerza con respecto al punto al cual se toma el momento por la fuerza.Explicado de una forma mas sencilla el torque es el producto entre la fuerza aplicada y la distancia a la cual se la aplica medida, generalmente, desde el punto que permanece fijo.
Así como una fuerza provoca una traslación, un torque produce una rotación.
El torque mide, de alguna manera, el estado de rotación que provoca la fuerza o la tendencia a producir una rotación.Del mismo modo que puede evitarse el desplazamiento de un objeto aplicando una fuerza contraria a la que lo hace mover, puede evitarse una rotación aplicando un torque contrario al que lo hace girar.
Ejemplos de rotacion y su fuerzas aplicadas
CONDICION DE EQUILIBRIO DE ROTACIÓN
Si a un cuerpo que puede girar alrededor de un eje, se la aplican varias fuerzas y no producen variación en su movimiento de rotación, se dice que el cuerpo puede estar en reposo o tener movimiento uniforme de rotación.
Para que exista este equilibrio se presentan los siguientes factores
a) Par de fuerzas: Se produce un par de fuerzas cuando dos fuerzas paralelas de la misma magnitud pero en sentido contrario actuan sobre un cuerpo, su resultante es igual a cero y su aplicacion esta en el centro de la linea que une los puntos de inicio de las fuerzas componentes.
b) Momento de una fuerza: Llamado tambien momento de torsion o torque y se define como la capacidad que tiene una fuerza para hacer girar un cuerpo, es decir es la intensidad con que una fuerza tiende a comunicarle un movimiento de rotacion. El momento de una fuerza se obtiene multiplicando el valor de la fuerza por su brazo de palanca.
c)Centro de gravedad.
El centro de gravedad (CG) es el punto de aplicación de la resultante de todas las fuerzas de gravedad que actúan sobre las distintas masas materiales de un cuerpo, de tal forma que el momento respecto a cualquier punto de esta resultante aplicada en el centro de gravedad es el mismo que el producido por los pesos de todas las masas materiales que constituyen dicho cuerpo. En otras palabras, el centro de gravedad de un cuerpo es el punto respecto al cual las fuerzas que la gravedad ejerce sobre los diferentes puntos materiales que constituyen el cuerpo producen un momento resultante nulo (dicho punto no necesariamente corresponde a un punto material del cuerpo, ya que puede estar situado fuera de él.
d)Equilibrio estático: existe un equilibrio estático cuando todas las fuerzas que actúan
sobre todos los componentes de un sistema están equilibradas.
e)Vectores: un vector es una magnitud que tiene dos características: módulo, o magnitud,
y dirección. Los vectores normalmente se dibujan como flechas. Una fuerza y el
momento de una fuerza son magnitudes vectoriales
Aplicaciones de el equilibrio rotacional
El equilibrio rotacional se puede aplicar en todo tipo de instrumentos en los cuales se requiera aplicar una o varias fuerzas o torques para llevar a cabo el equilibrio de un cuerpo. Entre los instrumentos más comunes están la palanca,la balanza romana, la polea, el engrane, etc.
Fricción
Definición:
La fricción es una fuerza de contacto que actúa para oponerse al movimiento deslizante entre superficies. Actúa paralela a la superficie y opuesta al sentido del deslizamiento. Se denomina como Ff . La fuerza de fricción también se le conoce como fuerza de rozamiento.
Contenido:
La fricción ocurre cuando dos objetos se deslizan entre sí o tienden a deslizarse. Cuando un cuerpo se mueve sobre una superficie o a través de un medio viscoso, como el aire o el agua, hay una resistencia al movimiento debido a que el cuerpo interactúa con sus alrededores. Dicha resistencia recibe también el nombre de fricción. Podemos observar el siguiente ejemplo:
Observa que el hombre realiza una fuerza sobre el objeto a la cual llamamos fuerza de empuje, también podemos llamarle fuerza aplicada. Podemos asumir que el objeto se desliza a la derecha, sin que haya rotación. La dirección de la fuerza, también es a la derecha, mientras que la fricción se dirige a la izquierda. En otras palabras la fuerza de fricción actúa paralela a la superficie y en contra del movimiento.
La forma general de escribir la ecuación para la fuerza de fricción es de la siguiente manera:
donde Ff es la fuerza de fricción mientras que μ es el coeficiente de fricción
Fricción estática
Ff=μsFN
Fricción cinética
Ff=μkFN
Coeficientes de fricción:
| Materiales en contacto | Fricción estática | Fricción cinética |
|---|---|---|
| Hielo // Hielo | 0.1 | 0.03 |
| Vidrio // Vidrio | 0.9 | 0.4 |
| Vidrio // Madera | 0.25 | 0.2 |
| Madera // Cuero | 0.4 | 0.3 |
| Madera // Piedra | 0.7 | 0.3 |
| Madera // Madera | 0.4 | 0.3 |
| Acero // Acero | 0.74 | 0.57 |
| Acero // Hielo | 0.03 | 0.02 |
| Acero // Latón | 0.5 | 0.4 |
| Acero // Teflón | 0.04 | 0.04 |
| Teflón // Teflón | 0.04 | 0.04 |
| Caucho // Cemento (seco) | 1.0 | 0.8 |
| Caucho // Cemento (húmedo) | 0.3 | 0.25 |
| Cobre // Hierro (fundido) | 1.1 | 0.3 |
| Esquí (encerado) // Nieve (0ºC) | 0.1 | 0.05 |
| Articulaciones humanas | 0.01 | 0.003 |
Coeficientes de fricción:
| Materiales en contacto | Fricción estática | Fricción cinética |
|---|---|---|
| Hielo // Hielo | 0.1 | 0.03 |
| Vidrio // Vidrio | 0.9 | 0.4 |
| Vidrio // Madera | 0.25 | 0.2 |
| Madera // Cuero | 0.4 | 0.3 |
| Madera // Piedra | 0.7 | 0.3 |
| Madera // Madera | 0.4 | 0.3 |
| Acero // Acero | 0.74 | 0.57 |
| Acero // Hielo | 0.03 | 0.02 |
| Acero // Latón | 0.5 | 0.4 |
| Acero // Teflón | 0.04 | 0.04 |
| Teflón // Teflón | 0.04 | 0.04 |
| Caucho // Cemento (seco) | 1.0 | 0.8 |
| Caucho // Cemento (húmedo) | 0.3 | 0.25 |
| Cobre // Hierro (fundido) | 1.1 | 0.3 |
| Esquí (encerado) // Nieve (0ºC) | 0.1 | 0.05 |
| Articulaciones humanas | 0.01 | 0.003 |
Trabajo: concepto en física
Energía, fuerza, potencia y eficiencia
Antes de explicar el concepto trabajo según lo describe o entiende la física, haremos un repaso o un recordatorio sobre aquella maravilla que mueve al mundo y que se denomina Energía.
Energía
Se define como energía aquella capacidad que posee un cuerpo (una masa) para realizar trabajo luego de ser sometido a una fuerza; es decir, el trabajo no sepuede realizar sin energía. Esta capacidad (la energía) puede estar dada por la posición de un cuerpo o por la velocidad del mismo; es por esto que podemos distinguir dos tipos de energía:
Energía potencial
Es la energía que posee un cuerpo (una masa) cuando se encuentra en posición inmóvil.
Por ejemplo, una lámpara colgada en el techo del comedor puede, si cae, romper la mesa. Mientras cuelga, tiene latente una capacidad de producir trabajo. Tiene energía en potencia, y por eso se le llama energía potencial.
De modo general, esto significa que un cuerpo de masa m colocado a una altura h, tiene una energía potencial calculable con la fórmula
La fórmula debe leerse como: energía potencial (Ep) es igual al producto de la masa (m) por la constante de gravedad (g = 10 m/s2) y por la altura (h).
La unidad de medida de la energía es la misma del trabajo, el Joule.
Referido a la energía, un Joule es la cantidad de energía necesaria para levantar un kilogramo masa a una altura de 10 cm de la superficie de la Tierra.
Otra unidad de energía son las calorías. Un Joule equivale a 0,24 calorías.
Si queremos pasar de Joules a calorías tan sólo multiplicaremos la cantidad por 0,24 y en el caso contrario la dividiremos por 0,24 obteniendo Joules.
 |
Ejercicio de práctica:
Un libro de 2 Kg reposa sobre una mesa de 80 cm, medidos desde el piso. Calcule la energía potencial que posee el libro en relación
a) con el piso
b) con el asiento de una silla, situado a 40 cm del suelo
Desarrollo:
Primero, anotemos los datos que poseemos:
m = 2 Kg (masa del libro)
h = 80 cm = 0,8 m (altura a la cual se halla el libro y desde donde “puede caer”)
g = 10 m/s2 (constante de gravedad) ( en realidad es 9,8)
Respecto a la silla:
h = 40 cm = 0,4 m (la diferencia entre la altura de la mesa y aquella de la silla)
Conocemos la fórmula para calcular le energía potencial (Ep):
Entonces, resolvemos:
Caso a)
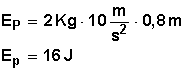
Respuesta: Respecto al piso (suelo), el libro tiene una energía potencial (Ep) de 16 Joules.
Caso b)
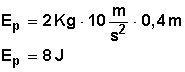
Respuesta: Respecto a la silla, el libro tiene una energía potencial (Ep) de 8 Joules.
Dato importante:
Recuerden que esta energía potencial calculada es eso: “potencial”, está almacenada o latente en el objeto inmóvil; pero OJO: se convierte en Energía cinética (Ec) si el objeto (en este caso el libro) cae al suelo (o sea, se mueve), en ese momento toda la Energía potencial que calculamos se convierte en Energía cinética (tiene el mismo valor calculado, en Joules).
|
Energía cinética
Es la misma energía potencial que tiene un cuerpo pero que se convierte en cinética cuando el cuerpo se pone en movimiento (se desplaza a cierta velocidad).
 |
| El viento mueve las aspas que rotan y producen nueva energía. |
Por ejemplo, para clavar un clavo hay que golpearlo con un martillo, pero para hacerlo el martillo debe tener cierta velocidad para impactar con fuerza en el clavo y realizar un trabajo, de esto se trata la energía cinética.
Claramente, debemos notar que aquí se ha incorporado el concepto develocidad.
Entonces, de modo general, un cuerpo de masa m que se mueve con velocidad v, tiene una energía cinética dada por la fórmula
Entonces, de modo general, un cuerpo de masa m que se mueve con velocidad v, tiene una energía cinética dada por la fórmula
Esta fórmula se lee como: Energía cinética (Ec) es igual a un medio (1/2 = 0,5) de la masa (m) multiplicado por la velocidad del cuerpo al cuadrado (v2).
Ejercicio de práctica:
Un macetero de 0,5 Kg de masa cae desde una ventana (donde estaba en reposo) que se encuentra a una altura de 4 metros sobre el suelo. Determine con qué velocidad choca en el suelo si cae.
Para resolver este problema veamos los datos de que disponemos:
Tenemos (m) la masa = 0,5 Kg
Tenemos (h) la altura desde la cual cae = 4 metros
Y conocemos la constante de gravedad (g) = 10 m/s2
Con estos datos podemos calcular de inmediato la energía potencial que posee el macetero antes de caer y llegar hasta el suelo, pues la fórmula es:
Reemplazamos lo valores en la fórmula y tenemos:
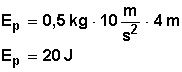
 |
| Asegurar los maceteros en las ventanas. |
Ahora bien, esta Energía potencial (20 Joules) se ha transformado enEnergía cinética desde el momento en que el macetero empezó a caer (a moverse) hacia la tierra, donde choca luego de recorrer la distancia (altura) desde su posición inicial (la ventana).
Por lo tanto, Energía potencial es igual a la Energía cinética, igual a 20 Joules
Ep = Ec = 20 J
Y como conocemos la fórmula para calcular la energía cinética
Reemplazamos y nos queda:
Con estos datos es claro que podremos despejar la ecuación para conocer la velocidad con la cual el macetero llega a la tierra (choca).
(Recordemos que ½ = 0,5)
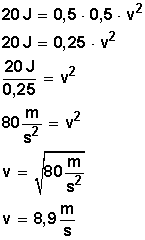
Respuesta: El macetero cae a tierra (choca) con una velocidad de 8,9 m/s
Trabajo
Ahora estamos en condiciones de referirnos al concepto trabajo.
Como idea general, hablamos de trabajo cuando una fuerza (expresada en newton) mueve un cuerpo y libera la energía potencialde este; es decir, un hombre o una maquina realiza un trabajo cuando vence una resistencia a lo largo de un camino.
Por ejemplo, para levantar una caja hay que vencer una resistencia, el peso P del objeto, a lo largo de un camino, la altura d a la que se levanta la caja. El trabajo T realizado es el producto de la fuerza P por la distancia recorrida d.
T = F · d Trabajo = Fuerza • Distancia
Aquí debemos hacer una aclaración.
Como vemos, y según la fórmula precedente, Trabajo es el producto (la multiplicación) de la distancia (d) (el desplazamiento) recorrida por un cuerpo por el valor de la fuerza (F) aplicada en esa distancia y es una magnitud escalar, que también se expresa enJoule (igual que la energía).
De modo más simple:
 |
| Este trabajo también equivale a la fuerza por la distancia. |
La unidad de trabajo (en Joule) se obtiene multiplicando la unidad de fuerza (en Newton) por la unidad de longitud (en metro).
Recordemos que el newton es la unidad de fuerza del Sistema Internacional (SI) que equivale a la fuerza necesaria para que un cuerpo de 1 kilogramo masa adquiera una aceleración de un metro por segundo cada segundo (lo mismo que decir “por segundo al cuadrado”). Su símbolo es N.
Por lo tanto, 1 joule es el trabajo realizado por una fuerza de 1 Newton al desplazar un objeto, en la dirección de la fuerza, a lo largo de 1 metro.
Aparece aquí la expresión “dirección de la fuerza” la cual puede ser horizontal. oblicua o vertical respecto a la dirección en que se mueve el objeto sobre el cual se aplica la fuerza.
En tal sentido, la “dirección de la fuerza” y la “dirección del movimiento” pueden formar un ángulo (o no formarlo si ambas son paralelas).
Si forman un ángulo (α), debemos incorporar ese dato en nuestra fórmula para calcular el trabajo, para quedar así:
Lo cual se lee: Trabajo = fuerza por coseno de alfa por distancia
OJO: El valor del coseno lo obtenemos usando la calculadora.
Si el ángulo es recto (90º) el coseno es igual a cero (0).
Si el ángulo es Cero (fuerza y movimiento son paralelos) el coseno es igual a Uno (1).
Nota:
En la fórmula para calcular el trabajo, algunos usan la letra W en lugar de T.
Así: W = F • cosα • d
Energía cinética final
Una variante para calcular el trabajo la tenemos cuando conocemos la Energía cinética final (Ecf) y conocemos la Energía cinética inicial (Eci) utilizando el Teorema trabajo-energía, expresado en la fórmula:
T = ½m vf2 –½m vi2 = Ecf – Eci = ΔEc (variación de energía cinética)
Que simplificada queda
T = Ecf – Eci
T = trabajo entre la posición final y la posición inicial
Ecf = energía cinética final
Eci = energía cinética inicial
Ecf = energía cinética final
Eci = energía cinética inicial
Usando esta fórmula, si conocemos el trabajo realizado y tenemos una de las energías cinéticas, se puede calcular la otra energía cinética.
Cuando la rapidez es constante, no hay variación de energía cinética y el trabajo de la fuerza neta es cero.
Ir a:
Ejercicios de aplicación sobre Trabajo, fuerza y energía
Ejercicio Nº 1
Ejercicio Nº 2
Ejercicio Nº 3
Ejercicio Nº 4
Ejercicio Nº 5
Ejercicio Nº 6
Potencia
Se denomina potencia al cuociente entre el trabajo efectuado y el tiempo empleado para realizarlo. En otras palabras, la potencia es el ritmo al que el trabajo se realiza. Un adulto es más potente que un niño y levanta con rapidez un peso que el niño tardará más tiempo en levantar.
La unidad de potencia se expresa en Watt, que es igual a 1 Joule por segundo,
Eficiencia
En física, la eficiencia o rendimiento de un proceso o de un dispositivo es la relación entre la energía útil y la energía invertida.
La parte de la energia que se pierde se disipa al ambiente en forma de calor
Potencia (física)
Si W es la cantidad de trabajo realizado durante un intervalo de tiempo de duración Δt, la potencia media durante ese intervalo está dada por la relación:
La potencia instantánea es el valor límite de la potencia media cuando el intervalo de tiempo Δt se aproxima a cero. En el caso de un cuerpo de pequeñas dimensiones:
Donde
- P es la potencia,
- W es el trabajo,
- t es el tiempo.
- r es el vector de posición.
- F es la fuerza.
- v es la velocidad.
Tipos de potencia[editar]
Potencia mecánica[editar]
La potencia mecánica aplicada sobre un sólido rígido viene dado por el producto de la fuerza resultante aplicada por la velocidad: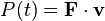 Si además existe rotación del sólido y las fuerzas aplicadas están cambiando su velocidad angular:
Si además existe rotación del sólido y las fuerzas aplicadas están cambiando su velocidad angular: donde:
donde: , son la fuerza resultante y el momento resultante.
, son la fuerza resultante y el momento resultante.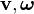 , son la velocidad del punto donde se ha calculado la resultante efectiva y la velocidad angular del sólido.
, son la velocidad del punto donde se ha calculado la resultante efectiva y la velocidad angular del sólido.
Para un sólido deformable o un medio continuo general la expresión es más compleja y se expresa como producto del tensor tensión y el campo de velocidades. la variación de energía cinética viene dada por: donde:
donde: , son las componentes del tensor de tensiones de Cauchy.
, son las componentes del tensor de tensiones de Cauchy.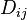 , son las componentes del tensor de velocidad de deformación.
, son las componentes del tensor de velocidad de deformación.
Potencia eléctrica[editar]
La potencia eléctrica P desarrollada en un cierto instante por un dispositivo viene dada por la expresión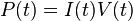 Donde:
Donde:- P(t) es la potencia instantánea, medida en vatios (julios/segundos).
- I(t) es la corriente que circula por él, medida en amperios.
- V(t) es la diferencia de potencial (caída de voltaje) a través del componente, medida en voltios.
Si el componente es una resistencia, tenemos: Donde:
Donde:- R es la resistencia, medida en ohmios.
Potencia sonora[editar]
La potencia del sonido, considerada como la cantidad de energía que transporta la onda sonora por unidad de tiempo a través de una superficie dada, depende de laintensidad de la onda sonora y de la superficie , viniendo dada, en el caso general, por: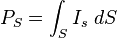
- Ps es la potencia
- Is es la intensidad sonora.
- dS es el elemento de superficie sobre alcanzado por la onda sonora.
Para una fuente aislada, el cálculo de la potencia sonora total emitida requiere que la integral anterior se extienda sobre una superficie cerrada.Unidades de potencia[editar]
- Sistema Internacional (SI):
- Vatio, (W):
- Sistema inglés:
- caballo de fuerza o de potencia, horsepower en inglés, (HP)
- 1 HP = 550 ft·lbf/s
- 1 HP = 745,699 871 582 270 22 W
- caballo de fuerza o de potencia, horsepower en inglés, (HP)
- Sistema técnico de unidades:
- kilográmetro por segundo, (kgm/s)
- 1 kgm/s = 9,80665 W
- kilográmetro por segundo, (kgm/s)
- Sistema cegesimal
- ergio por segundo, (erg/s)
- 1 erg/s = 1x10-7 W
- ergio por segundo, (erg/s)
- Otras unidades:
- caballo de vapor, (CV)
- 1 CV = 75 kgf·m/s = 735,49875 W
Energía potencial
- En un sistema físico, la energía potencial es la energía que mide la capacidad que tiene dicho sistema para realizar untrabajo en función exclusivamente de su posición o configuración. Puede pensarse como la energía almacenada en el sistema, o como una medida del trabajo que un sistema puede entregar. Suele abreviarse con la letra
 o
o  .La energía potencial puede presentarse como energía potencial gravitatoria, energía potencial electrostática, y energía potencial elástica.Más rigurosamente, la energía potencial es una magnitud escalar asociada a un campo de fuerzas (o como en elasticidad un campo tensorial de tensiones). Cuando la energía potencial está asociada a un campo de fuerzas, la diferencia entre los valores del campo en dos puntos A y B es igual al trabajo realizado por la fuerza para cualquier recorrido entre B y A.
.La energía potencial puede presentarse como energía potencial gravitatoria, energía potencial electrostática, y energía potencial elástica.Más rigurosamente, la energía potencial es una magnitud escalar asociada a un campo de fuerzas (o como en elasticidad un campo tensorial de tensiones). Cuando la energía potencial está asociada a un campo de fuerzas, la diferencia entre los valores del campo en dos puntos A y B es igual al trabajo realizado por la fuerza para cualquier recorrido entre B y A. 
 Los carros de una montaña rusaalcanzan su máxima energía potencialgravitacional en la parte más alta del recorrido. Al descender, ésta es convertida en energía cinética, la que llega a ser máxima en el fondo de la trayectoria (y la energía potencial mínima). Luego, al volver a elevarse debido a lainercia del movimiento, el traspaso de energías se invierte. Si se asume unafricción insignificante, la energía total del sistema permanece constante.
Los carros de una montaña rusaalcanzan su máxima energía potencialgravitacional en la parte más alta del recorrido. Al descender, ésta es convertida en energía cinética, la que llega a ser máxima en el fondo de la trayectoria (y la energía potencial mínima). Luego, al volver a elevarse debido a lainercia del movimiento, el traspaso de energías se invierte. Si se asume unafricción insignificante, la energía total del sistema permanece constante. Energía potencial asociada a campos de fuerzas[editar]
La energía potencial puede definirse solamente cuando la fuerza es conservativa. Si las fuerzas que actúan sobre un cuerpo son no conservativas, entonces no se puede definir la energía potencial, como se verá a continuación. Una fuerza es conservativa cuando se cumple alguna de las siguientes propiedades:- El trabajo realizado por la fuerza entre dos puntos es independiente del camino recorrido.
- El trabajo realizado por la fuerza para cualquier camino cerrado es nulo.
- Cuando el rotacional de la fuerza es cero.
Se puede demostrar que todas las propiedades son equivalentes (es decir, que cualquiera de ellas implica la otra). En estas condiciones, la energía potencial se define como: Si las fuerzas no son conservativas no existirá en general una manera unívoca de definir la anterior integral. De la propiedad anterior se sigue que si la energía potencial es conocida, se puede obtener la fuerza a partir del gradiente de U:
Si las fuerzas no son conservativas no existirá en general una manera unívoca de definir la anterior integral. De la propiedad anterior se sigue que si la energía potencial es conocida, se puede obtener la fuerza a partir del gradiente de U: También puede recorrerse el camino inverso: suponer la existencia una función energía potencial y definir la fuerza correspondiente mediante la fórmula anterior. Se puede demostrar que toda fuerza así definida es conservativa.La forma funcional de la energía potencial depende de la fuerza de que se trate; así, para el campo gravitatorio (o eléctrico), el resultado del producto de las masas (o cargas) por una constante dividido por la distancia entre las masas (cargas), por lo que va disminuyendo a medida que se incrementa dicha distancia.
También puede recorrerse el camino inverso: suponer la existencia una función energía potencial y definir la fuerza correspondiente mediante la fórmula anterior. Se puede demostrar que toda fuerza así definida es conservativa.La forma funcional de la energía potencial depende de la fuerza de que se trate; así, para el campo gravitatorio (o eléctrico), el resultado del producto de las masas (o cargas) por una constante dividido por la distancia entre las masas (cargas), por lo que va disminuyendo a medida que se incrementa dicha distancia.Energía potencial gravitatoria[editar]
La energía potencial gravitatoria es la energía asociada con la fuerza gravitatoria. Esta dependerá de la altura relativa de un objeto a algún punto de referencia, la masa, y la fuerza de la gravedad.Por ejemplo, si un libro apoyado en una mesa es elevado, una fuerza externa estará actuando en contra de la fuerza gravitacional. Si el libro cae, el mismo trabajo que el empleado para levantarlo, será efectuado por la fuerza gravitacional.Por esto, un libro a un metro del piso tiene menos energía potencial que otro a dos metros, o un libro de mayor masa a la misma altura.Si bien la fuerza gravitacional varía con la distancia (altura), en las proximidades de la superficie de la Tierra la diferencia es muy pequeña como para ser considerada, por lo que se considera a la aceleración de la gravedad como una constante (9,8 m/s2) en cualquier parte. En cambio en la Luna, cuya gravedad es muy inferior, se generaliza el valor de 1,66 m/s2Para estos casos en los que la variación de la gravedad es insignificante, se aplica la fórmula: Sin embargo, si la distancia (la variación de altitud) es importante, y por tanto la variación de la aceleración de la gravedad es considerable, se aplica la fórmula general:
Sin embargo, si la distancia (la variación de altitud) es importante, y por tanto la variación de la aceleración de la gravedad es considerable, se aplica la fórmula general: Donde
Donde es la energía potencial,
es la energía potencial,  es la distancia entre la partícula material y el centro de la Tierra,
es la distancia entre la partícula material y el centro de la Tierra, 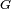 la constante universal de la gravitación y
la constante universal de la gravitación y 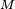 la masa de la Tierra. Esta última es la fórmula que necesitamos emplear, por ejemplo, para estudiar el movimiento de satélites y misiles balísticos:
la masa de la Tierra. Esta última es la fórmula que necesitamos emplear, por ejemplo, para estudiar el movimiento de satélites y misiles balísticos:Cálculo simplificado[editar]
Cuando la distancia recorrida por un móvil, h, es pequeña, lo que sucede en la mayoría de las aplicaciones usuales (tiro parabólico, saltos de agua, etc.), podemos usar el desarrollo de Taylor a la anterior ecuación. Así si llamamos r a la distancia al centro de la Tierra, R al radio de la Tierra y h a la altura sobre la superficie de la Tierra, es decir, r = R + h tenemos: Donde hemos introducido la aceleración sobre la superficie:
Donde hemos introducido la aceleración sobre la superficie: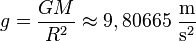 Por tanto la variación de la energía potencial gravitatoria al desplazarse un cuerpo de masa m desde una altura h1 hasta una altura h2 es:
Por tanto la variación de la energía potencial gravitatoria al desplazarse un cuerpo de masa m desde una altura h1 hasta una altura h2 es:
Dado que la energía potencial se anula cuando la distancia es infinita, frecuentemente se asigna energía potencial cero a la altura correspondiente a la del suelo, ya que lo que es de interés no es el valor absoluto de U, sino su variación durante el movimiento.Así, si la altura del suelo es h1 = 0, entonces la energía potencial a una altura h2 = h será simplemente UG = mgh.Energía potencial electrostática[editar]
La energía potencial electrostática de un sistema formado por dos partículas de cargas q y Q situadas a una distancia r una de la otra es igual a: Siendo K la constante de Coulomb, una constante universal cuyo valor aproximado es 9×109 (voltios·metro/culombio).
Siendo K la constante de Coulomb, una constante universal cuyo valor aproximado es 9×109 (voltios·metro/culombio).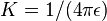 donde ε es la permitividad del medio. En el vacío ε = ε0 = 8,85x10-12 (culombio/voltio·metro)..Una definición de energía potencial eléctrica sería la siguiente: cantidad de trabajo que se necesita realizar para acercar una carga puntual de masa nula con velocidad constante desde el infinito hasta una distancia r de una carga del mismo signo, la cual utilizamos como referencia. En el infinito la carga de referencia ejerce una fuerza nula.Es importante no confundir la energía potencial electrostática con el potencial eléctrico, que es el trabajo por unidad de carga:
donde ε es la permitividad del medio. En el vacío ε = ε0 = 8,85x10-12 (culombio/voltio·metro)..Una definición de energía potencial eléctrica sería la siguiente: cantidad de trabajo que se necesita realizar para acercar una carga puntual de masa nula con velocidad constante desde el infinito hasta una distancia r de una carga del mismo signo, la cual utilizamos como referencia. En el infinito la carga de referencia ejerce una fuerza nula.Es importante no confundir la energía potencial electrostática con el potencial eléctrico, que es el trabajo por unidad de carga: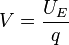
Energía potencial elástica[editar]
La energía elástica o energía de deformación es el aumento de energía interna acumulada en el interior de un sólido deformable como resultado del trabajo realizado por las fuerzas que provocan la deformación.Potencial armónico[editar]
El Potencial armónico (caso unidimensional), dada una partícula en un campo de fuerzas que responda a la ley de Hooke, como el caso de un muelle se puede calcular estimando el trabajo necesario para mover la partícula una distancia x:si es un muelle ideal cumpliría la ley de Hooke:El trabajo desarrollado (y por tanto la energía potencial) que tendríamos sería:Las unidades están en julios. La sería la constante elástica del muelle o del campo de fuerzas.
sería la constante elástica del muelle o del campo de fuerzas.Energía de deformación[editar]
La energía de deformación (caso lineal): en este caso la función escalar que da el campo de tensiones es la energía libre de Helmholtz por unidad de volumen, f, que representa la energía de deformación. Para un sólido elástico lineal e isótropo, la energía potencial elástica en función de las deformaciones εij y la temperatura la energía libre de un cuerpo deformado viene dada por:(1)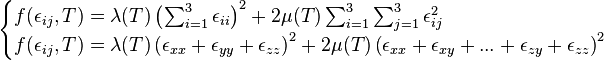 Donde
Donde son constantes elásticas llamadas coeficientes de Lamé, que pueden depender de la temperatura, y están relacionadas con el módulo de Young y el coeficiente de Poisson mediante las relaciones algebraicas:
son constantes elásticas llamadas coeficientes de Lamé, que pueden depender de la temperatura, y están relacionadas con el módulo de Young y el coeficiente de Poisson mediante las relaciones algebraicas: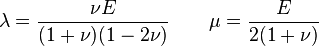 A partir de esta expresión () del potencial termodinámico de energía libre pueden obtenerse las tensiones a partir de las siguientes relaciones termodinámicas:
A partir de esta expresión () del potencial termodinámico de energía libre pueden obtenerse las tensiones a partir de las siguientes relaciones termodinámicas: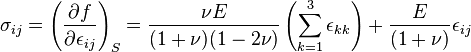 Estas últimas ecuaciones se llaman ecuaciones de Lamé-Hooke y escritas más explícitamente en forma matricial tienen la forma:Donde
Estas últimas ecuaciones se llaman ecuaciones de Lamé-Hooke y escritas más explícitamente en forma matricial tienen la forma:Donde- Energía de deformación (caso no lineal general), en el caso de materiales elásticos no lineales la energía de deformación puede definirse sólo en el caso demateriales hiperelásticos. Y en ese caso la energía elástica está estrechamente relacionada con el potencial hiperelástico a partir de la cual se deduce la ecuación constitutiva.
- Energía Cinética (Ec)
Cuando un cuerpo está en movimiento posee energía cinética ya que al chocar contra otro puede moverlo y, por lo tanto, producir un trabajo.Para que un cuerpo adquiera energía cinética o de movimiento; es decir, para ponerlo en movimiento, es necesario aplicarle una fuerza. Cuanto mayor sea el tiempo que esté actuando dicha fuerza, mayor será la velocidad del cuerpo y, por lo tanto, su energía cinética será también mayor.Otro factor que influye en la energía cinética es la masa del cuerpo.Por ejemplo, si una bolita de vidrio de 5 gramos de masa avanza hacia nosotros a una velocidad de 2 km / h no se hará ningún esfuerzo por esquivarla. Sin embargo, si con esa misma velocidad avanza hacia nosotros un camión, no se podrá evitar la colisión.La fórmula que representa la Energía Cinética es la siguiente:E c = 1 / 2 • m • v 2E c = Energía cinéticam = masav = velocidadCuando un cuerpo de masa m se mueve con una velocidad v posee una energía cinética que está dada por la fórmula escrita más arriba.En esta ecuación, debe haber concordancia entre las unidades empleadas. Todas ellas deben pertenecer al mismo sistema. En elSistema Internacional (SI), la masa m se mide en kilogramo (kg) y la velocidad v en metros partido por segundo ( m / s), con lo cual la energía cinética resulta medida en Joule ( J ).









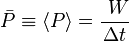


 es la energía potencial,
es la energía potencial,  la
la 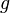 la aceleración de la
la aceleración de la 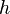 la altura.
la altura.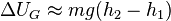





No hay comentarios:
Publicar un comentario