Fuerza eléctrica
Entre dos o más cargas aparece una fuerza denominada fuerza eléctrica cuyo módulo depende de el valor de las cargas y de la distancia que las separa, mientras que su signo depende del signo de cada carga. Las cargas del mismo signo se repelen entre sí, mientras que las de distinto signo se atraen.
La fuerza entre dos cargas se calcula como:


q1, q2 = Valor de las cargas 1 y 2
d = Distancia de separación entre las cargas
Fe = Fuerza eléctrica


q1, q2 = Valor de las cargas 1 y 2
d = Distancia de separación entre las cargas
Fe = Fuerza eléctrica
La fuerza es una magnitud vectorial, por lo tanto además de determinar el módulo se deben determinar dirección y sentido.
Dirección de la fuerza eléctrica
Si se trata únicamente de dos cargas, la dirección de la fuerza es colineal a la recta que une ambas carga.
Sentido de la fuerza eléctrica
El sentido de la fuerza actuante entre dos cargas es de repulsión si ambas cargas son del mismo signo y de atracción si las cargas son de signo contrario.
Fuerzas originadas por varias cargas sobre otra
Si se tienen varias cargas y se quiere hallar la fuerza resultante sobre una de ellas, lo que se debe hacer es plantear cada fuerza sobre la carga (una por cada una de las otras cargas). Luego se tienen todas las fuerzas actuantes sobre esta carga y se hace la composición de fuerzas, con lo que se obtiene un vector resultante.
Campo eléctrico
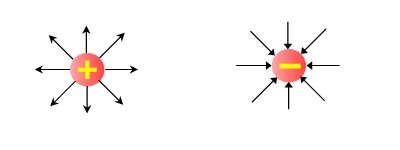
El campo eléctrico existe cuando existe una carga y representa el vínculo entre ésta y otra carga al momento de determinar la interacción entre ambas y las fuerzas ejercidas. Tiene carácter vectorial (campo vectorial) y se representa por medio de líneas de campo. Si la carga es positiva, el campo eléctrico es radial y saliente a dicha carga. Si es negativa es radial y entrante.
La unidad con la que se mide es:

La letra con la que se representa el campo eléctrico es la E.
Al existir una carga sabemos que hay un campo eléctrico entrante o saliente de la misma, pero éste es comprobable únicamente al incluir una segunda carga (denominada carga de prueba) y medir la existencia de una fuerza sobre esta segunda carga.

La letra con la que se representa el campo eléctrico es la E.
Al existir una carga sabemos que hay un campo eléctrico entrante o saliente de la misma, pero éste es comprobable únicamente al incluir una segunda carga (denominada carga de prueba) y medir la existencia de una fuerza sobre esta segunda carga.
Algunas características
- En el interior de un conductor el campo eléctrico es 0.
- En un conductor con cargas eléctricas, las mismas se encuentran en la superficie.
- En un conductor con cargas eléctricas, las mismas se encuentran en la superficie.
El potencial eléctrico en un punto es el trabajo que debe realizar una fuerza eléctrica para mover una carga positiva q desde la referencia hasta ese punto, dividido por unidad de carga de prueba. Dicho de otra forma, es el trabajo que debe realizar una fuerza externa para traer una carga unitaria q desde la referencia hasta el punto considerado en contra de la fuerza eléctrica.

Considérese una carga puntual de prueba positiva, la cual se puede utilizar para hacer el mapa de un campo eléctrico. Para tal carga de prueba localizada a una distancia r de una carga q, la energía potencial electrostática mutua es:
De manera equivalente, el potencial eléctrico es


Considérese una carga puntual de prueba positiva, la cual se puede utilizar para hacer el mapa de un campo eléctrico. Para tal carga de prueba localizada a una distancia r de una carga q, la energía potencial electrostática mutua es:
De manera equivalente, el potencial eléctrico es

Trabajo eléctrico y energía potencial eléctrica
Considérese una carga puntual q en presencia de un campo eléctrico. La carga experimentará una fuerza eléctrica. Se define como el trabajo "W"

Ahora bien, si se pretende mantener la partícula en equilibrio, o desplazarla a velocidad constante, se requiere de una fuerza que contrarreste el efecto de la generada por el campo eléctrico. Esta fuerza deberá tener la misma magnitud que la primera, pero sentido contrario, es decir: (1)
(1)

Ahora bien, si se pretende mantener la partícula en equilibrio, o desplazarla a velocidad constante, se requiere de una fuerza que contrarreste el efecto de la generada por el campo eléctrico. Esta fuerza deberá tener la misma magnitud que la primera, pero sentido contrario, es decir:
 (1)
(1)Diferencia de Potencial eléctrico
Considérese una carga de prueba positiva en presencia de un campo eléctrico y que se traslada desde el punto A al punto B conservándose siempre en equilibrio. Si se mide el trabajo que debe hacer el agente que mueve la carga, la diferencia de potencial eléctrico se define como:

El trabajo uede ser positivo, negativo o nulo. En estos casos el potencial eléctrico en B será respectivamente mayor, menor o igual que el potencial eléctrico en A. La unidad en el SI para la diferencia de potencial que se deduce de la ecuación anterior es Joule/Coulomb y se representa mediante una nueva unidad, el voltio, esto es: 1 voltio = 1 joule/coulomb.
Usualmente se escoge el punto A a una gran distancia (en rigor el infinito) de toda carga y el potencial eléctrico esta distancia infinita recibe arbitrariamente el valor cero. Esto permite definir el potencial eléctrico en un punto poniendo eliminando los índices:
eliminando los índices:

siendo l trabajo que debe hacer un agente exterior para mover la carga de prueba esde el infinito al punto en cuestión.
Obsérvese que la igualdad planteada depende de que se da arbitrariamente el valor cero al potencial n la posición de referencia (el infinito) el cual hubiera podido escogerse de cualquier otro valor así como también se hubiera podido seleccionar cualquier otro punto de referencia.

El trabajo uede ser positivo, negativo o nulo. En estos casos el potencial eléctrico en B será respectivamente mayor, menor o igual que el potencial eléctrico en A. La unidad en el SI para la diferencia de potencial que se deduce de la ecuación anterior es Joule/Coulomb y se representa mediante una nueva unidad, el voltio, esto es: 1 voltio = 1 joule/coulomb.
Usualmente se escoge el punto A a una gran distancia (en rigor el infinito) de toda carga y el potencial eléctrico esta distancia infinita recibe arbitrariamente el valor cero. Esto permite definir el potencial eléctrico en un punto poniendo
 eliminando los índices:
eliminando los índices:
siendo l trabajo que debe hacer un agente exterior para mover la carga de prueba esde el infinito al punto en cuestión.
Obsérvese que la igualdad planteada depende de que se da arbitrariamente el valor cero al potencial n la posición de referencia (el infinito) el cual hubiera podido escogerse de cualquier otro valor así como también se hubiera podido seleccionar cualquier otro punto de referencia.
Capacitancia
1.- ¿Qué es capacitancia?
Se define como la razón entre la magnitud de la carga de cualquiera de los conductores y la magnitud de la diferencia de potencial entre ellos.
La capacitancia siempre es una cantidad positiva y puesto que la diferencia de potencialaumenta a medida que la carga almacenada se incrementa, la proporción Q / V es constante para un capacitor dado. En consecuencia la capacitancia de un dispositivo es una medida de su capacidad para almacenar carga y energía potencial eléctrica.
La capacitancia tiene la unidad del SI coulomb por volt. La unidad de capacitancia del SI es el farad (F), en honor a Michael Faraday.
CAPACITANCIA = 1F = 1 C
1 V
El farad es una unidad de capacitancia muy grande. En la práctica los dispositivos comunes tienen capacitancia que varían de microfarads a picofarads.
La capacitancia de un dispositivo depende entre otras cosas del arreglo geométrico de los conductores.
2.- ¿Qué es un capacitor?
Considere dos conductores que tienen una diferencia de potencial V entre ellos. Supongamos que tienen cargas iguales y opuestas, como en la figura. Una combinación de este tipo se denomina capacitor . La diferencia de potencial V es proporcional a la magnitud de la carga Q del capacitor.(Esta puede probarse por la Ley de coulomb o a través de experimentos.
-Qjg
Un capacitor se compone de dos conductores aislados eléctricamente uno del otro y de sus alrededores. Una vez que el capacitor se carga, los dos conductores tienen cargas iguales pero opuestas.
3.- ¿Cuáles son los tipos de capacitores?
Los capacitores comerciales suelen fabricarse utilizando láminas metálicas intercaladas con delgadas hojas de papel impregnado de parafina o Mylar, los cuales sirvan como material dieléctrico. Estas capas alternadas de hoja metálica y dieléctrico después se enrollan en un cilindro para formar un pequeño paquete. Los capacitores de alto voltaje por lo común constan de varias placas metálicas entrelazadas inmersas en aceite de silicón. Los capacitores pequeños en muchas ocasiones se construyen a partir de materiales cerámicos. Los capacitores variables (comúnmente de 10 a500 pF) suelen estar compuestos de dos conjuntos de placas metálicas entrelazadas, uno fijo y el otro móvil, con aire como el dieléctrico.
Un capacitor electrolítico se usa con frecuencia para almacenar grandes cantidades de carga a voltajes relativamente bajos. Este dispositivo, mostrado en la figura consta de una hoja metálica en contacto con un electrolito, es decir, una solución que conduce electricidad por virtud del movimiento de iones contenidos en la solución. Cuando se aplica un voltaje entre la hoja y el electrolito, una delgada capa de óxido metálico (un aislador) se forma en la hoja y esta capa sirve como el dieléctrico. Pueden obtenerse valores muy grandes de capacitancia debido a que la capa del dieléctrico es muy delgada y por ello la separación de placas es muy pequeña.
Cuando se utilizan capacitores electrolíticos en circuitos , la polaridad (los signos más y menos en el dispositivo) debe instalarse de manera apropiada. Si la polaridad del voltaje es aplicado es opuesta a la que se pretende, la capa de óxido se elimina y el capacitor conduce electricidad en lugar de almacenar carga.
Placas
Lamina electrolito caso
metálica
Contactos
Aceite Línea metálica
Papel +capa de óxido
- Capacitor de placas paralelas
Dos placas paralelas de igual área A están separadas por una distancia d, como en la figura. Una placa tiene carga Q, la otra carga -Q. La carga por unidad de área sobre cualquier placa es = Q /A. Si las placas están muy cercanas una de la otra (en comparación con su longitud y ancho), podemos ignorar los efectos de borde y suponer que el campo eléctrico es uniforme entre las placas y cero en cualquier otra parte.
El campo eléctrico entre las placas es:
E = = Q donde o es:
o oA 8.85*10-12
Donde o es la permitividad del espacio libre. La diferencia de potencial entre las placas es igual a Ed; por lo tanto,
V =Ed = Qd
oA
Al sustituir este resultado en la ecuación de capacitancia, encontramos que la capacitancia es igual a,
C = Q = __Q_____
V Qd / oA
Es decir, la capacitancia de un capacitor de placas paralelas es proporcional al área de sus placas e inversamente proporcional a la separación de estas.
+ Q
- Q
Area = A
d
Un capacitor de placas paralelas se compone de dos placas paralelas cada una de área A, separadas por una distancia d. Cuando se carga el capacitor, las cargas tienen cargas iguales de signo opuesto.
- Capacitor cilíndrico
Un conductor cilíndrico de radio a y carga Q es coaxial con un cascaron cilíndrico más grande de radio b y carga -Q con una longitud l.
Suponiendo que l es grande comparada con a,b, podemos ignorar los efectos del borde. En este caso, el campo es perpendicular a los ejes de los cilindros y está confinado a la región entre ellos ;como se ve en la figura. Se debe calcular primero la diferencia de potencial entre los dos cilindros, la cual está dada por lo general por
b
Vb - Va = "a E * ds
Donde E es el campo eléctrico en la región a<r<b. Utilizando la ley de Gauss se demostró que el campo eléctrico de un cilindro de carga por unidad de longitud es E = 2ke / r. El mismo resultado se aplica aquí debido a que el cilindro exterior no contribuye al campo eléctrico dentro de él. Con este resultado y notando que E esta a lo largo de r en la figura encontramos que:
b b
Vb - Va = "a Er dr = -2ke "a dr / r =-2ke ln(b / a)
Al sustituir esto en la ecuación de capacitancia y utilizando el hecho de que =Q /l obtenemos:
C = Q = ______Q_______ = ________l_____
V 2ke ln (b) 2ke ln (b)
l (a) (a)
Donde V es la magnitud de la diferencia de potencial, dada por 2ke ln (b/a), una cantidad positiva. Es decir V =Va -Vb es positiva debido a que el cilindro interior está a un potencial mayor. El resultado nos muestra que la capacitancia es proporcional a la longitud de los cilindros. La capacitancia en este caso depende de los radios de los cilindros conductores.
l
b)
a) Superficie gausiana
a)El capacitor cilíndrico se compone de un conductor cilíndrico de radio a y la longitud l rodeado por un cascaron cilíndrico coaxial de radio b.
b)Vista lateral de un capacitor cilíndrico. La línea punteada representa el final de la superficie gaussiana cilíndrica de radio r y longitud l.
- Capacitor esférico
Un capacitor esférico consta de un cascarón esférico de radio b y carga -Q concéntrico con una esfera conductora más pequeña de radio a y carga Q.
El campo fuera de una distribución de carga simétrica esfericamente es radial y está dado por ke Q / r2. En este caso, corresponde al campo entre las esferas (a<r<b). (El campo es cero en cualquier otro lado). De la ley de Gauss vemos que sólo la esfera interior contribuye a este campo. De este modo, la diferencia de potencial entre las esferas está dada por
b b b
Vb - Va = - "a Er dr = keQ "a dr /r2 =keQ[1/r]a
Vb - Va = keQ(1 / b -1/ a)
La magnitud de la diferencia de potencial es:
V = Va -Vb = kQ (b - a)
ab
Sustituyendo esto en la ec. de capacitancia, obtenemos
- Q
Un capacitor esférico consta de una esfera interior de radio a rodeada por un casacaron esférico de radio b. El campo eléctrico entre las esfera apunta radialmente hacia fuera si la esfera interior está cargada positivamente.
Combinaciones de capacitores
Es común que dos o más capacitores se combinen de varias maneras . La capacitancia equivalente de ciertas combinaciones puede calcularse utilizando métodos como son la combinación en paralelo o en serie. Los símbolos de circuitos para capacitores y baterías, junto con sus códigos de color, se muestran en la figura. La terminal positiva de la batería esta al potencial más alto y se representa por la línea vertical más larga en el símbolo de la batería.
Símbolo de Símbolo de Símbolo de
Capacitor batería interruptor
- +
se nota que los capacitores están en verde y las baterías y los interruptores en verde.
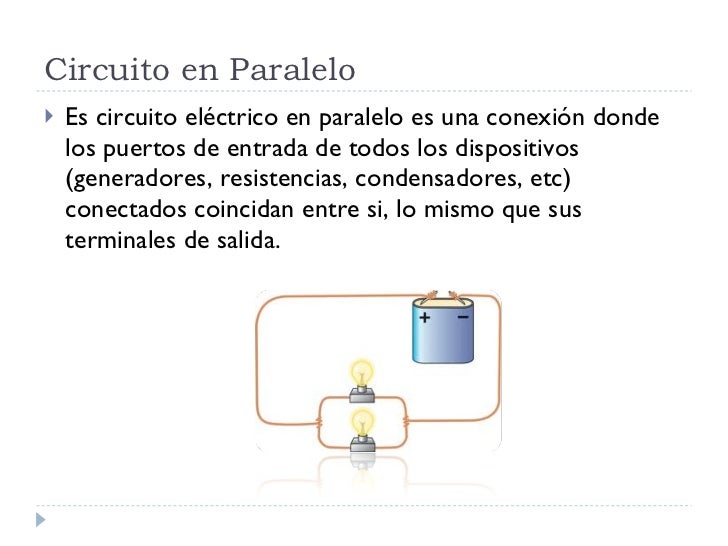
Combinación en paralelo
La diferencia de potencial que existe es a través de cada capacitor en el circuito paralelo es la misma e igual a l voltaje de la batería.
C1
Q1
C2
Q2
+ -
V
Combinación en serie
Para está combinación en serie de capacitores, la magnitud de la carga debe ser la misma en todas las placas.
V1 C1 V2 C2
+Q -Q +Q -Q
+ -
V
También existen capacitores con dieléctricos (que es un material no conductor como, el caucho, vidrio o papel). Cuando un material dieléctrico se inserta entre las placas de un capacitor aumenta la capacitancia. Si el dieléctrico llena por completo el espacio entre las placas, la capacitancia aumenta en un factor adimensional K, conocido como la constante dieléctrica.
Dieléctrico
Co
+ - Qo
V
4.-Menciona dos ejemplos de calculo de capacitancia:
Problema 1
Un capacitor de placas paralelas tiene un área A = 2.00 * 10-4 m2 y una separación de placa d =1.00mm. encuentre su capacitancia.
C = oA
d
C = (8.85*10-12C2/N* m2) (2.00*10-4 m2 /1.00*10-3m)
C =1.77 * 10-12 F = 1.77 pF
Si la separación se incrementa a 3.00mm determine la capacitancia
C = (8.85*10-12C2/N* m2) (2.00*10-4 m2 /3.00*10-3m)
C =0.590 pF
Problema 2
Las placas de un capacitor de placas paralelas miden 2.0 cm * 3.0 cm y están separadas por un espesor de papel de 1.0 mm.
Determine la capacitancia de este dispositivo.(puesto que K =3.7 para el papel)
C =K oA
d
C =3.7 (8.85*10-12C2/N* m2) (6.0*10-4 m2 /1.0*10-3m)
C =20 * 10-12 F =20 pF
Electricidad y Magnetismo
- Q
+Q
C = oA
d
C =Q
V
C =________l_____
2ke ln (b)
(a)
b
a
r Q
b
a
C =Q = ab
V ke (b-a)
Ceq = C1 + C2
ó
Ceq = C1 + C2 + C3 + ...
1 = 1 + 1 + 1 + ....
Ceq C1 C2 C3
C =K oA
d
Se denomina corriente eléctrica al flujo de carga eléctrica a través de un material sometido a una diferencia de potencial.
Históricamente, se definió como un flujo de cargas positivas y se fijó el sentido convencional de circulación de la corriente como un flujo de cargas desde el polo positivo al negativo. Sin embargo, posteriormente se observó, gracias al efecto Hall, que en los metales los portadores de carga son electrones, con carga negativa, y se desplazan en sentido contrario al convencional.

La intensidad de corriente (I) en una sección dada de un conductor (s) se define como la carga eléctrica (Q) que atraviesa la sección en una unidad de tiempo (t):

Corriente Continúa y Alterna

Introducción
En la se conoce poco en las instituciones educativas, esto si por parte del estudiantado sobre la conceptualización de términos técnicos en los que se encierran funcionalidades de las que depende en gran medida el sistema de las masas que es la sociedad y lo que equipara como complemento para la subsistencia tanto de subsistemas que dependen de la electricidad tales como el industrial y sus formas de uso como principio para el inicio de la sostenibilidad.
Cuando se conocía poco acerca del sistema eléctrico, el ser humano tenía que limitarse tan solo al uso de esa electricidad sin entenderla pero como ahora es posible el enlace entre la conceptualización y la aplicación de los elementos que conforman el sistema eléctrico, se favorece a la comprensión de la estructura y funcionalidad de dicho recurso.
Corriente continua (CC)
Es el flujo continuo de electrones a través de un conductor entre dos puntos de distinto potencial, en ella las cargas eléctricas circulan siempre en la misma dirección (es decir, los terminales de mayor y de menor potencial son siempre los mismos). Aunque comúnmente se identifica la corriente continúa con la corriente constante (por ejemplo la suministrada por una batería), es continua toda corriente que mantenga siempre la misma polaridad.

Descubrimiento
Su descubrimiento se remonta a la invención de la primera pila por parte del científico Conde Alessandri Volta.

Usos
Tras el descubrimiento de Thomas Alva Edison de la generación de electricidad en las postrimerías del siglo XIX, la corriente continua comenzó a emplearse para la transmisión de la energía eléctrica. Ya en el siglo XX este uso decayó en favor de la corriente alterna por sus menores pérdidas en la transmisión a largas distancias, si bien se conserva en la conexión de líneas eléctricas de diferente frecuencia y en la transmisión a través de cables submarinos.
La corriente continua es empleada en infinidad de aplicaciones y aparatos de pequeño voltaje alimentados con baterías (generalmente recargables) que suministran directamente corriente continua, o bien con corriente alterna como es el caso, por ejemplo, de los ordenadores, siendo entonces necesario previamente realizar la conversión de la corriente alterna de alimentación en corriente continua.
También se está extendiendo el uso de generadores de corriente continua mediante células solares, dado el nulo impacto medioambiental del uso de la energía solar frente a las soluciones convencionales (combustible fósil y energía nuclear).
Conversión de (C.A) a (C.C):
Muchos aparatos necesitan corriente continua para funcionar, sobre todos los que llevan electrónica (equipos , ordenadores, etc.). Para ellos se utilizan fuentes de alimentación que rectifican y convierten la tensión a una adecuada. Este proceso, denominado rectificación, consta de tres etapas. En una primera etapa, se rectifica la señal convirtiendo la negativa en positiva al tiempo que se disminuye la diferencia de potencial empleando un transformador. Posteriormente se realiza un filtrado que disminuye el rizado de la señal pulsante rectificada obteniendo una señal triangular. Finalmente la señal se nivela obteniendo una salida continua constante.
 | ||||
? Rectificado ?
|
? Nivelado ?
| |||
 |
? Filtrado ?
|  | ||
Las teconologías disponibles para la rectificación están basadas en el empleo de diodos (caso de la figura) o tiristores. En este último caso, la potencia de salida es regulable por lo que se emplean en numerosas aplicaciones industriales, por ejemplo, en los que es necesario regular la temperatura en función del uso, lo que no puede hacerse empleando simples diodos.
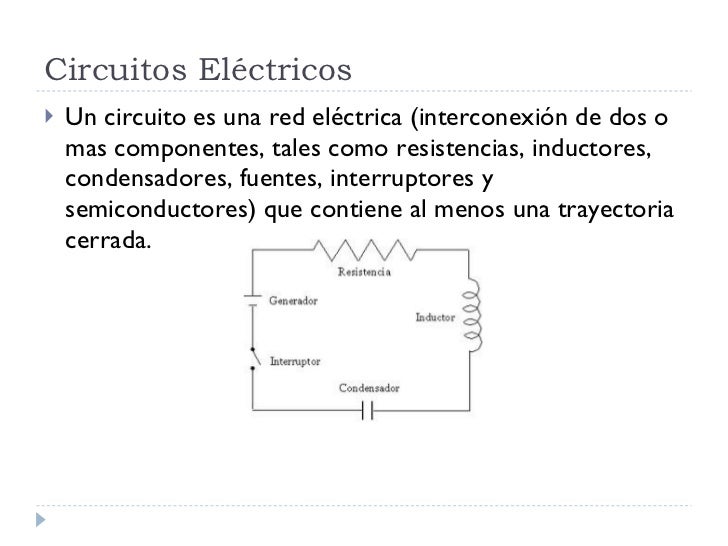
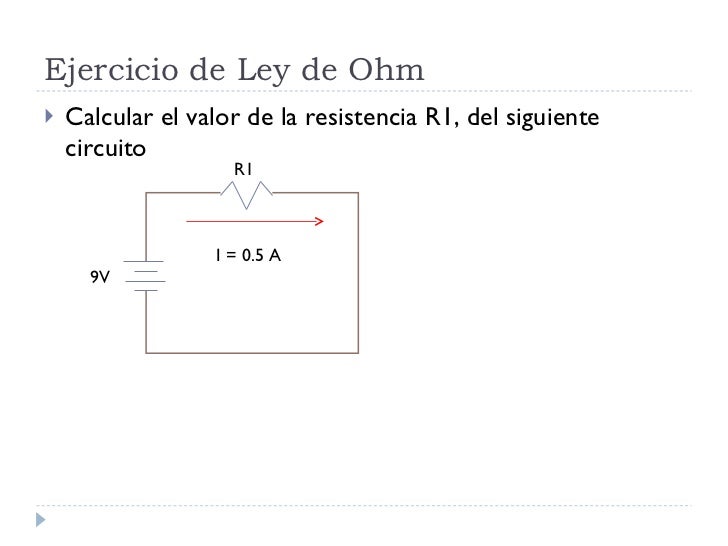
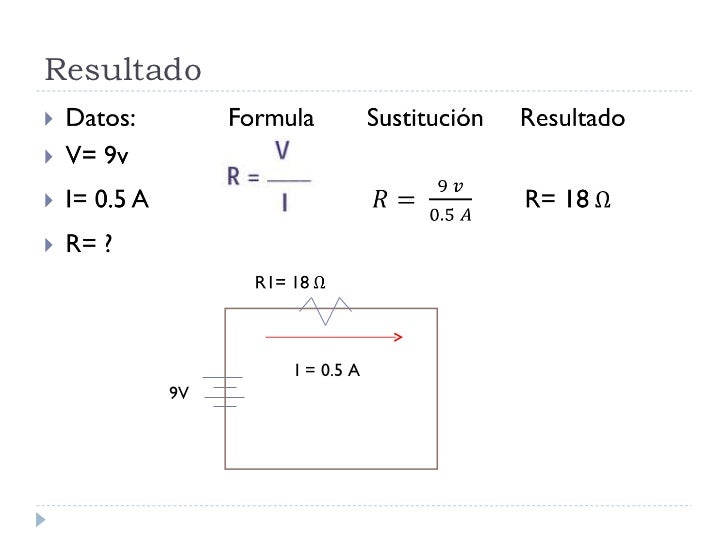
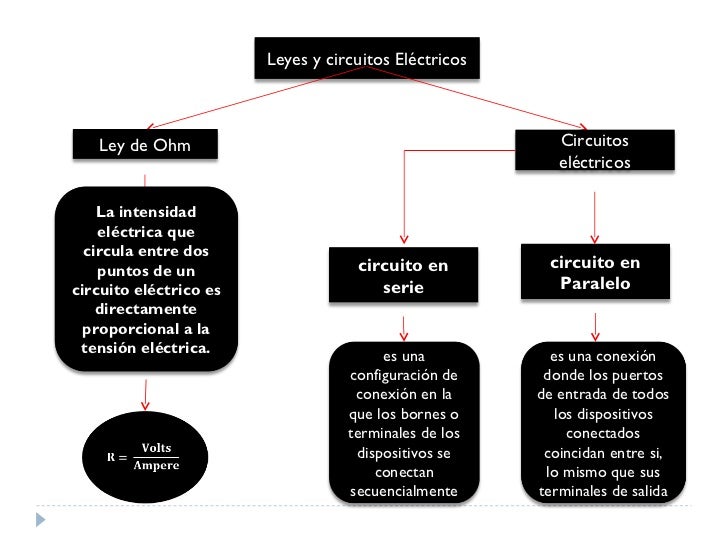
Leyes Eléctricas.











No hay comentarios:
Publicar un comentario